Large-scale Data-Informed Screening Under Population Heterogeneity
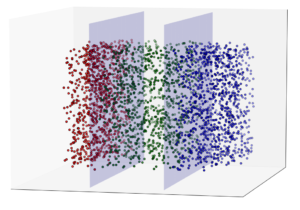
The design of large-scale screening strategies is an essential aspect of accurate and efficient classification of large populations for a binary characteristic (e.g., presence of an infectious disease, a genetic disorder, or a product defect). The performance of screening strategies heavily depends on various population-level characteristics that often vary, sometimes substantially, by individuals. Available datasets provide crucial, yet often neglected, information on population heterogeneity, and incorporating such information into the testing designs is of utmost importance, as failing to do so leads to strategies with higher classification errors and costs. A natural question arises: How does one optimally incorporate population heterogeneity into the mathematical framework to obtain optimal data-informed screening schemes? This research has received limited attention in the literature due to the resulting difficult combinatorial optimization problems. In this project, we theoretically prove that a sub-class of these optimization problems, which were once claimed to be intractable, can be cast as network flow problems (e.g., constrained shortest path), significantly improving the computational tractability. This, in turn, leads to polynomial time algorithms capable of handling realistic instances of the problem. Further, we investigate important, yet often neglected, dimensions of screening, such as equity/fairness and robustness. Our empirical results, from publicly available datasets (e.g., Centers for Disease Control and Prevention), demonstrate how data-informed screening strategies have the potential to significantly reduce screening costs and improve classification accuracy over current screening practices.
Robust Testing Designs for Time-varying and Dynamic Environments
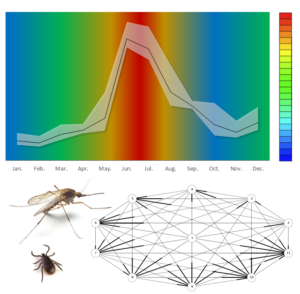
Categorical Clustering Procedure for Population Risk-class Classification
