Since joining Texas A&M University as an assistant professor, I have eagerly immersed myself in numerous exciting projects. Allow me to elaborate on three noteworthy endeavors below.
Data Analytics and Optimization for Mitigating the University Mental Health Crisis
The mental health crisis has emerged as a significant public health challenge, affecting a substantial portion of the American population. According to the National Institute of Mental Health, one in five American adults grapples with a diagnosable mental illness, highlighting the urgency of the situation. This crisis has a disproportionate impact on specific demographics, particularly young adults aged between 18 and 25 years old, resulting in a surge of cases on university campuses. As a consequence, there has been an increased reliance on campus Counseling and Psychological Services (CAPS) centers among students seeking help. Unfortunately, the demand for mental health services has far exceeded the available resources, leading to limited access to crucial support and adversely affecting student outcomes. The research objective of this project is to establish novel data analytics and optimization techniques that harness outcome- and provider-based data to construct maximally effective treatments, increase students’ access to services, and strike a balance between operational efficiency and treatment effectiveness. Our team is closely collaborating with domain experts, including Texas A&M’s CAPS center, as well as the Center for Collegiate Mental Health (CCMH), which is a nationwide large-scale network of over 750 CAPS centers.
At the core of the problem lies a complex stochastic system characterized by various system-centric attributes (see figure). This system involves multiple customer classes with distinct non-stationary arrival processes and diverse counselors who offer a range of services. A treatment plan consists of a sequence of sessions, each defined by counselor and service allocation, and the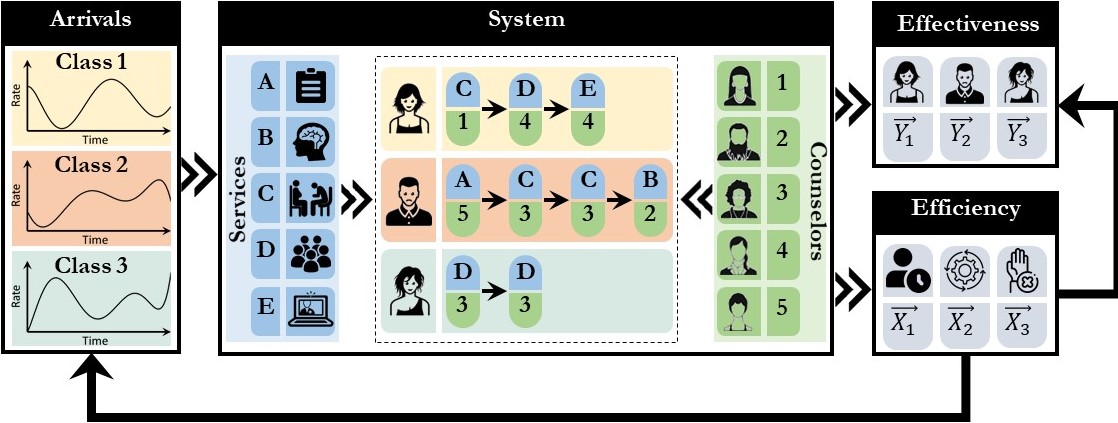 
number of sessions depends on the individual’s needs. The performance of the system depends on the arrivals and the provision of treatment, with key performance metrics being operational efficiency and treatment effectiveness. The efficiency of the system impacts both the arrivals and the effectiveness of treatment, introducing endogenous uncertainty and interdependence among these performance metrics. What sets this stochastic system apart is the intricate nature of mental health, which necessitates careful measurement of progress and evaluation of treatment effectiveness. Mishandling cases in this context can have severe consequences such as self-harm or harm to others, further highlighting the uniqueness of the problem. A rigorous analysis of this system holds the promise to overcome the barriers hindering progress in addressing the crisis. This undertaking requires scientific advancements in the analysis of temporally correlated data, time series forecasting, surrogate modeling, combinatorial optimization, global programming, and simulation optimization. The project consists of three primary research thrusts, each focused on an unresolved question that poses a significant obstacle to progress in addressing the crisis.
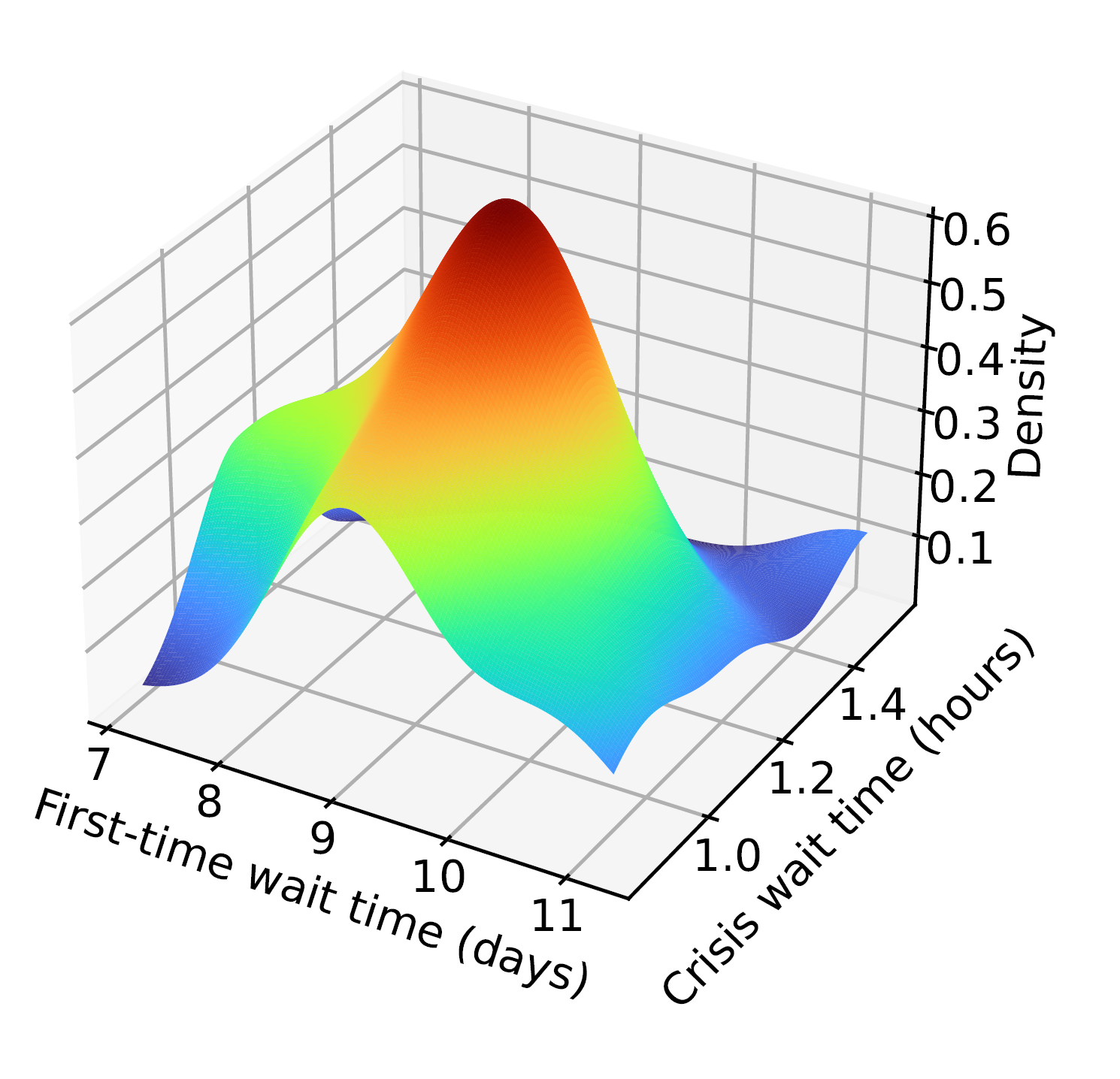
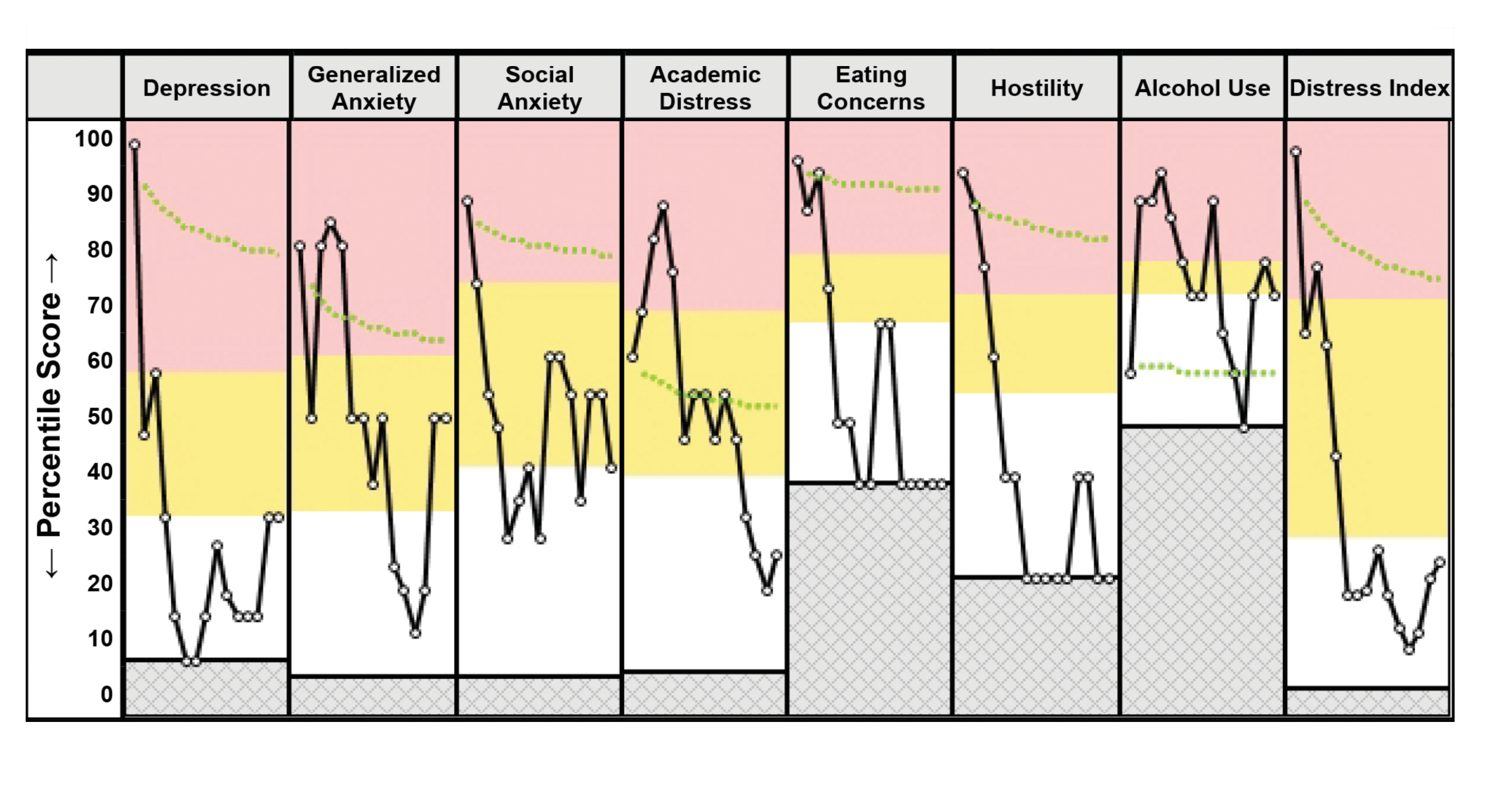Question 1: How to Quantify/Predict Treatment Effectiveness? Student responses to treatments can exhibit significant variability, as what proves effective for one student may yield suboptimal results for another. Therefore, it is crucial to quantify and comprehend the diverse effectiveness of different treatments in order to effectively address the crisis at hand. Our team is collaborating with psychologists and analyzing student outcome data obtained from CCAPS-34 reports (see figure to the right). CCAPS-34 is a widely recognized and extensively utilized tool that pro
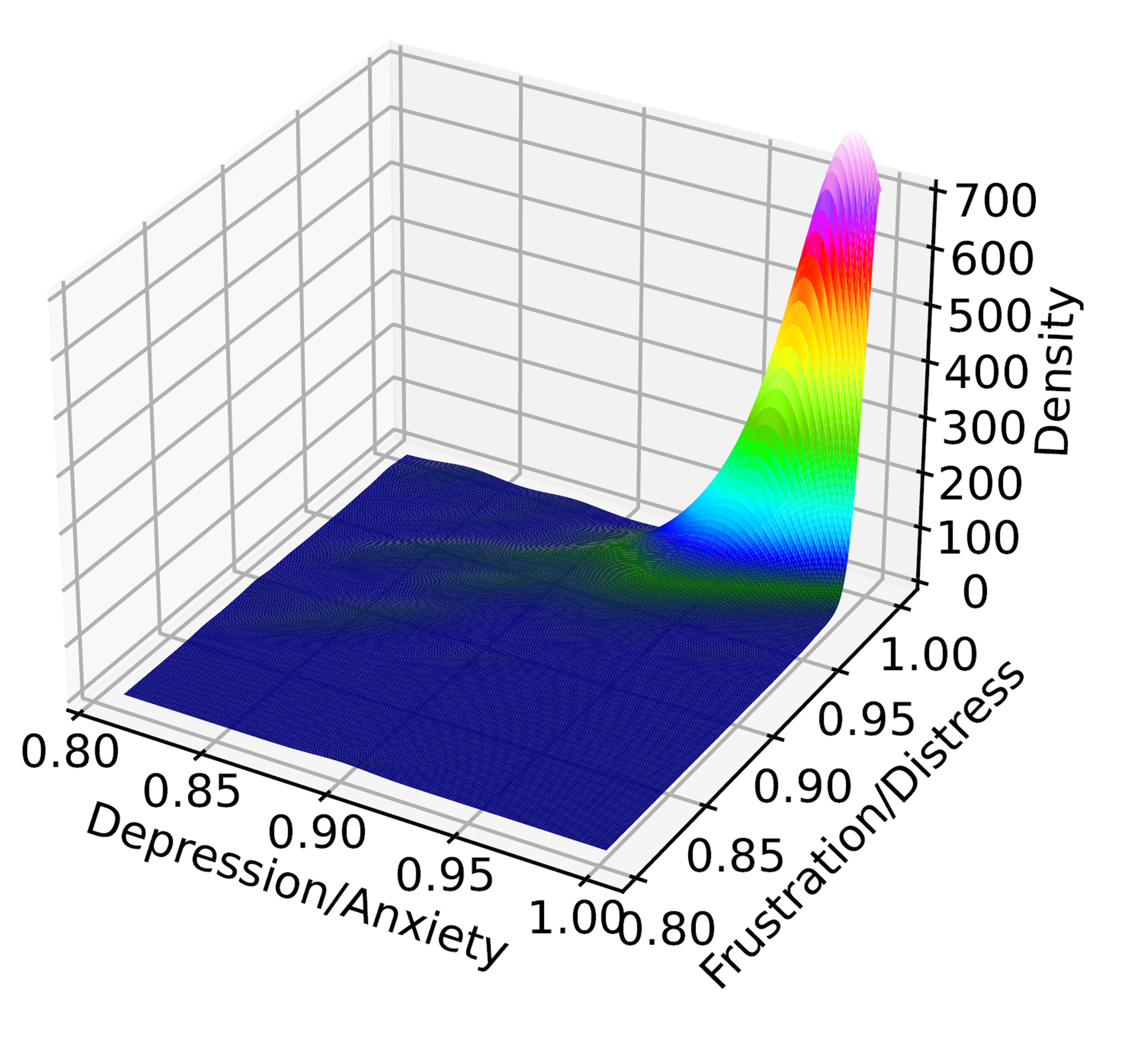vides percentile scores for key psychological symptoms based on a 34-question survey that takes three minutes. The tool is allowing us to monitor the impact of treatments on different psychological symptoms. Combining CCAPS-34 with student information and treatment history is resulting in a multidimensional outcome dataset (see figure to the left). Our team is currently establishing a novel Gaussian process regression technique that incorporates time-varying covariants to predict students’ responses to treatments. We are using this technique to inform an innovative Bayesian optimization-based active learning technique capable of handling non-scalar responses and discrete variables to optimize student outcomes. The resulting problem is being solved via a spatial branching scheme based on a new class of convex underestimators, which will enable us to construct maximally effective treatment plans that are tailored to handle each student’s specific needs.
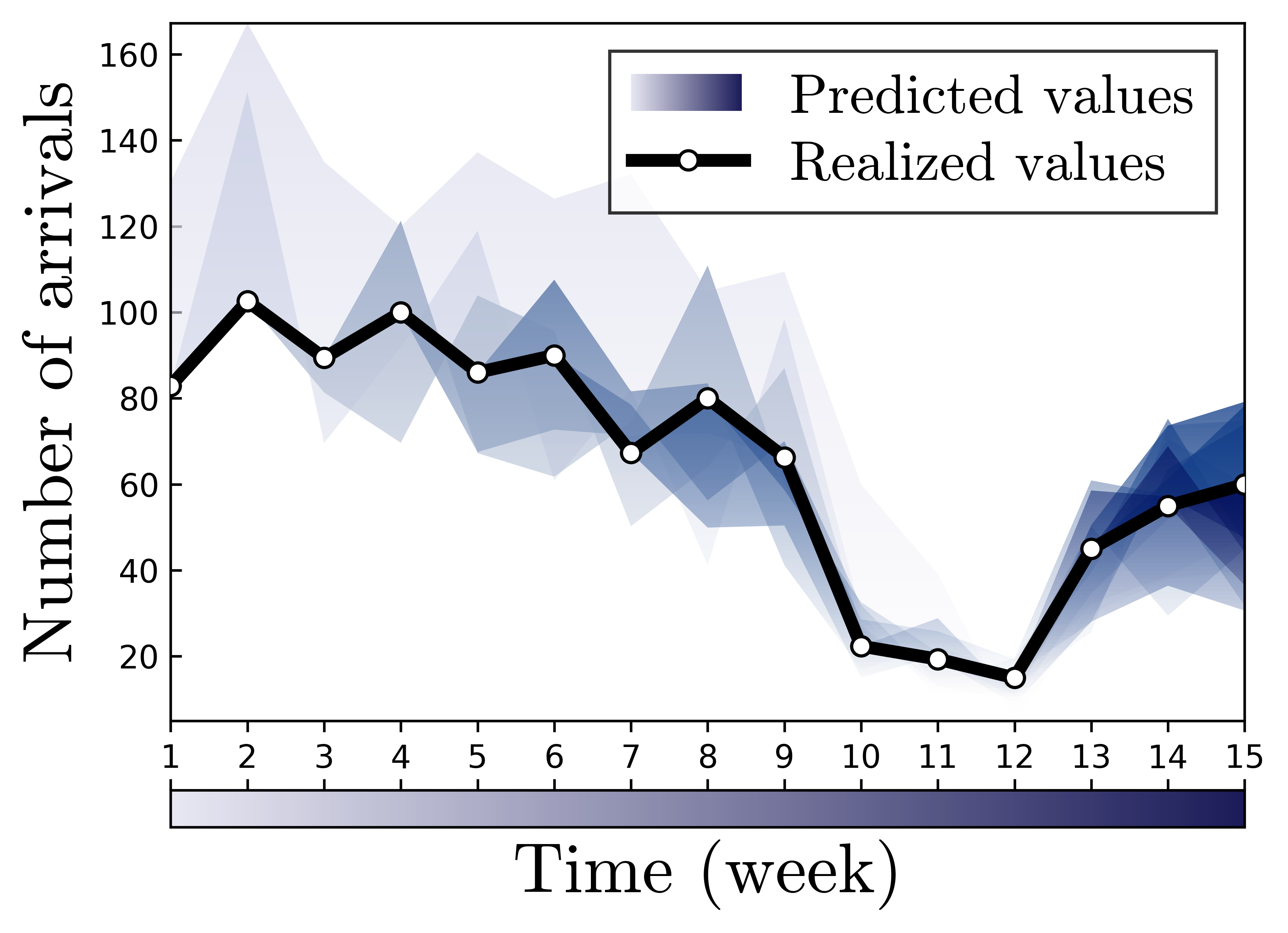Question 2: How to improve access to care? Even before the onset of COVID-19’s negative impact, the average nationwide wait time for CAPS was already 2 weeks. The unresolved crisis persists due to the lack of prompt access to services, despite the availability of effective treatments. CAPS centers currently lack comprehensive mental health data on students seeking services for the first time. Moreover, the arrival behavior of these students may be influenced by their unobserved state and the system’s efficiency, leading to endogenous uncertainty. To address these challenges, our team has developed a groundbreaking autoregressive time series forecasting approach. This innovative approach incorporates non-stationary trends, interdimensional dependencies, 
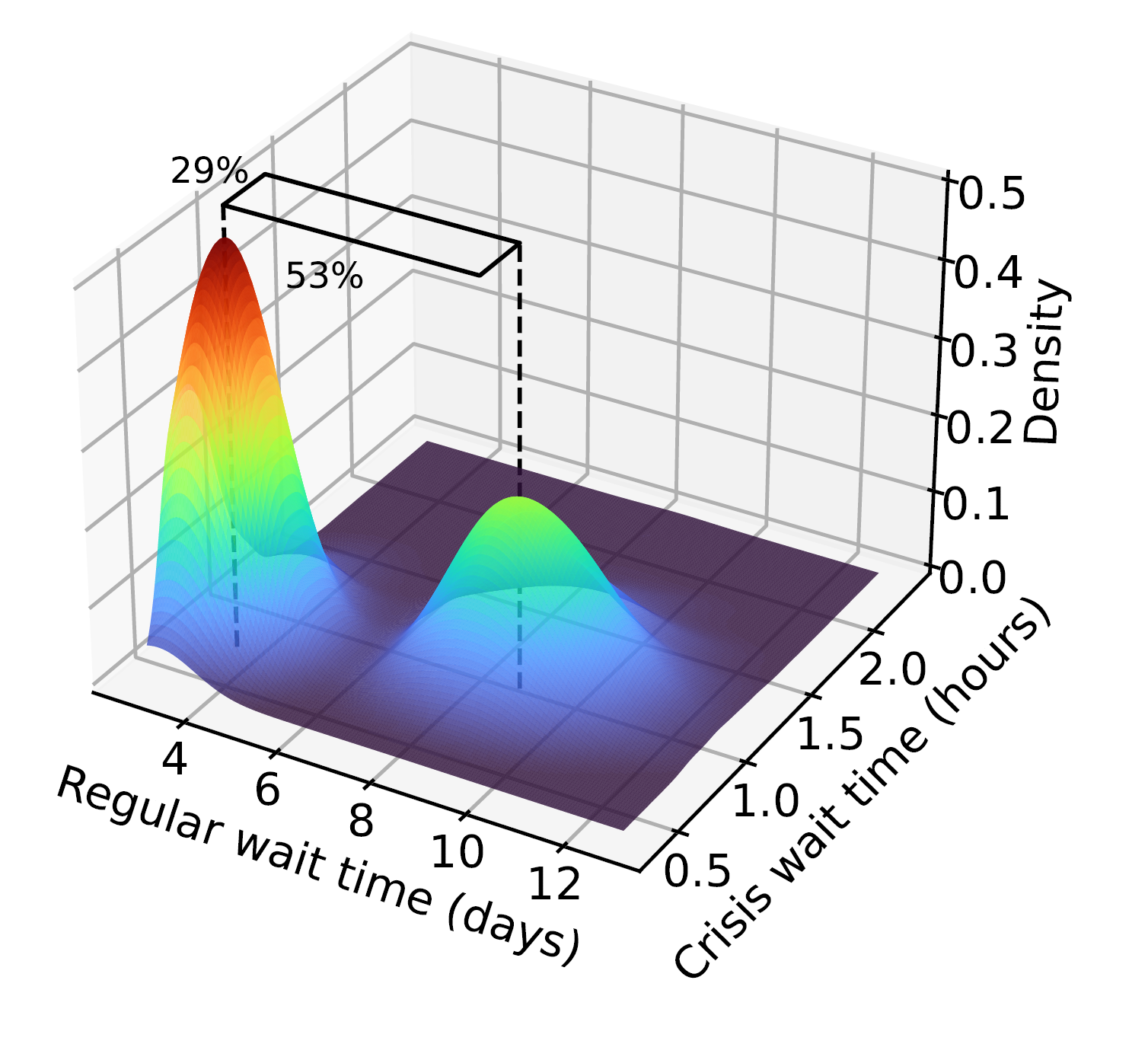and endogeneity, offering a more data-efficient, interpretable, and tractable alternative to deep neural networks. By leveraging historical demand patterns, our forecasting model accurately predicts future arrivals, which are periodically updated as new data becomes available (see figure to the right). Furthermore, we integrate this forecasting model into a stochastic system, where its transient behavior is approximated using our novel Pointwise Transient Approximation (PTA) scheme, which has been proven to be asymptotically correct. This system is optimized through a unique multivariate set partitioning-based solution scheme, resulting in scheduling policies that enhance new users’ access to critical mental health care services. Our results demonstrate the remarkable effectiveness of this approach in reducing wait times compared to current practices. For regular and crisis patients, we achieved a significant reduction of 53% and 29% (see figure to the left), respectively, highlighting the exciting potential of this project.
Question 3: How to balance operational efficiency and treatment effectiveness? Enhancing treatment effectiveness by increasing the number of sessions for each student comes at the cost of consuming more limited resources, which reduces access to care for students seeking CAPS services for the first time. To effectively address this crisis, it is essential to consider both efficiency and effectiveness. To optimize the delicate equilibrium between these tradeoffs, our team skillfully merged the active learning model and the treatment effectiveness forecasting model into a discrete event simulation model. This integrated model allows us to evaluate operational efficiency and treatment effectiveness simultaneously. By optimizing this simulation model, we can identify Pareto optimal solutions where further improvement in one criterion cannot be achieved without sacrificing the other. Identifying the efficiency-effectiveness Pareto frontier is crucial for finding solutions that strike a balance between operational efficiency and treatment effectiveness. However, constructing the Pareto frontier requires repeated optimization of this large-scale simulation model, which is both expensive and challenging. To overcome this obstacle, our team is currently developing a novel surrogate modeling technique using deep Gaussian processes (DGPs). This approach enables us to estimate the simulation’s response by capturing a broad range of probability functions and characterizing the entire output distribution efficiently. Moreover, it handles large simulations with non-scalar outputs effectively (see figure). Using this surrogate model, we have devised two innovative surrogate simulation optimization techniques based on stochastic approximation and sample average approximation. These techniques leverage DGPs to optimize large-scale and expensive simulations efficiently. Employing these methods will enable us to construct the Pareto frontier efficiently, providing valuable insights into the trade-offs between operational efficiency and treatment effectiveness. Ultimately, we aim to offer CAPS directors data-driven guidelines to enhance their systems based on these insights.
Data-Driven Strategies for Optimizing Spatiotemporal Infectious Outbreak Response
Effectively controlling and monitoring infectious diseases is essential to prevent outbreaks and the severe socio-economic impacts that accompany them. The swift global spread and high fatality rate of COVID-19 highlight the shortcomings of insufficient disease management. Emerging new variants compound the problem, underscoring global unpreparedness for such extensive outbreaks. Experts have sounded alarms about the potential for even more serious outbreaks, emphasizing the dire need to enhance preparedness measures. Notably, the last 150 years have seen an unparalleled number of outbreaks, with over half transpiring in the past two decades. While improved detection methods account for some of this increase, population growth and the rise of pathogen-handling labs have also elevated outbreak risks. Given the expert consensus and the evidence pointing to a rising frequency of outbreaks, a transformative preparedness platform is crucial. The World Health Organization has stated that it would take 500 years of preparedness investment to offset the losses incurred from COVID-19. Recognizing this urgency, the Federal government has initiated a program to pioneer advances that will reshape the nation’s strategy in combating biological threats. The aim of this project is to support the success of this initiative with innovative data-driven spatiotemporal strategies to optimally monitor and control infectious disease outbreaks.
The project connects research with practice, facilitating the rapid translation of theoretical discoveries into real-world implementations. Our collaborative team is actively engaged with the University of Texas Medical Branch (UTMB), leveraging their extensive repository of COVID-19 Electronic Medical Record (EMR) data for a retrospective evaluation study. Moreover, UTMB serves as a strategic hub for the National Institute of Allergy and Infectious Diseases (NIAID), specifically the West African Center for Emerging Infectious Diseases. This center strives to tackle the transmission of diseases from animals to humans and the subsequent consequences. The research endeavors within this project, coupled with UTMB’s domain expertise and data accessibility, are being harnessed to develop guidelines for establishing a network of laboratories and hospitals equipped to promptly and effectively respond to future zoonotic outbreaks. Zoonotic viral surveillance assumes a pivotal role in preempting the recurrence of viruses like SARS-CoV-2, Ebola, and HIV, all of which originated from animals. By closely monitoring viruses present in animal populations, we can curtail the impact of zoonotic diseases on both human and animal health, proactively preventing or controlling their transmission. Furthermore, zoonotic viral surveillance provides valuable insights into the epidemiology and evolution of such viruses, enabling the formulation of robust prevention and control strategies. The significance of early detection in averting potential outbreaks cannot be overstated, as it can make the difference between containing an outbreak and facing a global pandemic. The project encompasses three primary research thrusts, each dedicated to addressing an unresolved question.
The project encompasses three primary research directions, each dedicated to addressing an unresolved question. Collectively, these research directions require innovations in discrete/continuous programming, epidemiology, optimal control problems, and unsupervised machine learning.
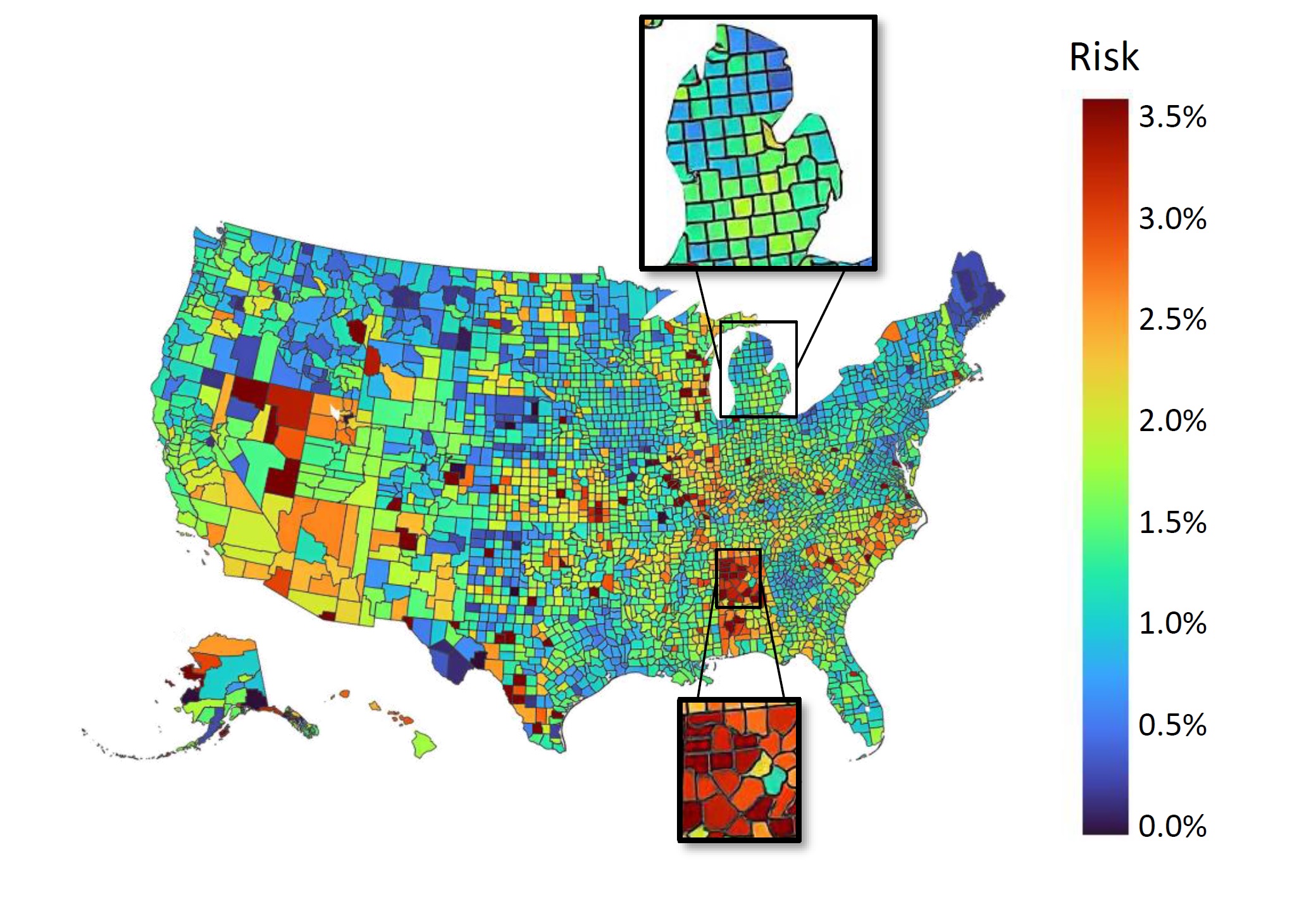Thrust 1: Learn Spatial Heterogeneity. The variability of risk, defined as the probability of having the infectious disease, among individuals presents both challenges and opportunities. For instance, we have observed significant differences in COVID-19 risk levels across the United States (see figure to the right). Identifying maximally heterogeneous sub-groups with the largest possible risk variation is crucial for practical feasibility. Defining each individual as a separate sub-group, for instance, yields the highest granularity, but raises tractability and practicality concerns. Policies based on such a granular decomposition may be infeasible, hindering effective decision-making. Broader sub-group definitions could still capture a significant level of heterogeneity without added complexity. By exploring sub-group formations that strike a balance between granularity and practicality, insights about a heterogeneous population can be extracted without sacrificing methodological rigor or practical feasibility. However, this requires addressing a robust clustering problem—a type of combinatorial optimization problem that is notably challenging to solve. Our team has pioneered a new method to address this challenge using an innovative, globally convergent solution scheme rooted in optimal orderings. More precisely, we employing a continuous relaxation of the problem to derive an equivalent linear form. Although the specific linear function is unknown, this alternate representation allows us to identify conditions that must hold in an optimal solution. These insights are then utilized to cast the problem as an equivalent and tractable network problem, which is solvable in polynomial time.
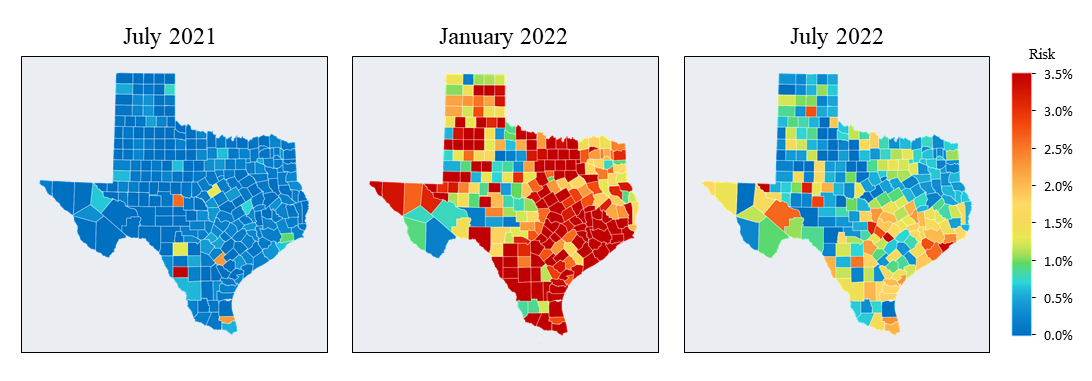Thrust 2: Infectious Outbreak Evolution. Infectious disease outbreaks exhibit significant spatial and temporal variability, characterized by complex evolution across regions with multiple interrelated waves. Their dynamics are influenced by various factors, including contact patterns across regions, contagiousness of the disease, and heterogeneous behavioral feedback. The COVID-19 pandemic serves as a prime example, with numerous waves of the outbreak observed across diverse geographic areas (see figure to the right). To effectively mitigate outbreaks, it is crucial to comprehend the intricate dynamics of disease spread, encompassing contagiousness and human behavior. Relying on inadequate models can result in ineffective mitigation efforts, underscoring the urgent necessity for innovative approaches that accurately capture the complex outbreak dynamics to inform policy decisions. Our team has established an innovative adaptive epidemiological spread model that integrates behavioral feedback to accurately depict the multi-wave progression of outbreaks. This novel model can account for variations in disease transmission, 
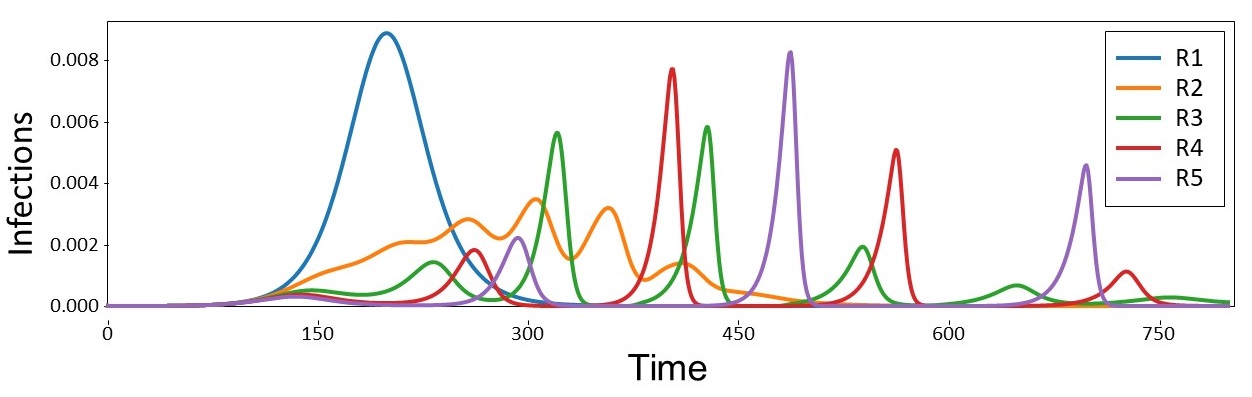progression, and severity across sub-groups, as well as interactions between sub-groups through contact patterns represented by a mixing matrix. Furthermore, the model incorporates heterogeneous behavioral feedback obtained from Thrust 1, enabling it to capture multi-wave patterns across diverse geographic regions. Through simulation results, the model has demonstrated its capability to accurately represent complex multi-wave dynamics across distinct regions (see figure to the left). This capacity to capture such dynamics accurately will play a pivotal role in identifying effective spatiotemporal mitigation measures.
Thrust 3: Optimal Spatiotemporal Mitigation Measures. Using the subgroups identified in Thrust 1, coupled with the infectious outbreak model of Thrust 2, we have established an optimization-based approach to identify spatiotemporal mitigation measures that best curb the transmission of the disease. Our team has developed several innovative solution techniques to address different variations of this challenging optimal control problem. For example, we have introduced a novel parameterized reformulation technique that transforms a class of mixed-integer nonlinear programs into a sequence of more tractable univariate optimization problems. By proving the unimodality of each problem through stochastic programming theory, we can pinpoint globally optimal solutions without relying on derivative-based methods. In another instance, we leverage closed-form characterizations of optimal mitigation designs established by our research team. We use these characterizations to examine the binding status of resource constraints, identify thresholds for resource levels, and determine optimal policies for each. Using this information, coupled with Pontryagin’s Principle, we identify optimality conditions which we embed into a Sequential Coordinate Descent approach that alternates between two modules. This procedure essentially linearizes all terms in the optimization stage, allowing the problem to be solved efficiently. Numerical experiments reveal that our spatiotemporal mitigation measures (see figure to the right) result in a substantial reduction of 52% in peak infections and 47% in total infections. These promising results demonstrate the significant potential of this project in effectively curbing the transmission of infectious outbreaks.
Global Optimization via Convex Relaxation-Based Spatial Branching
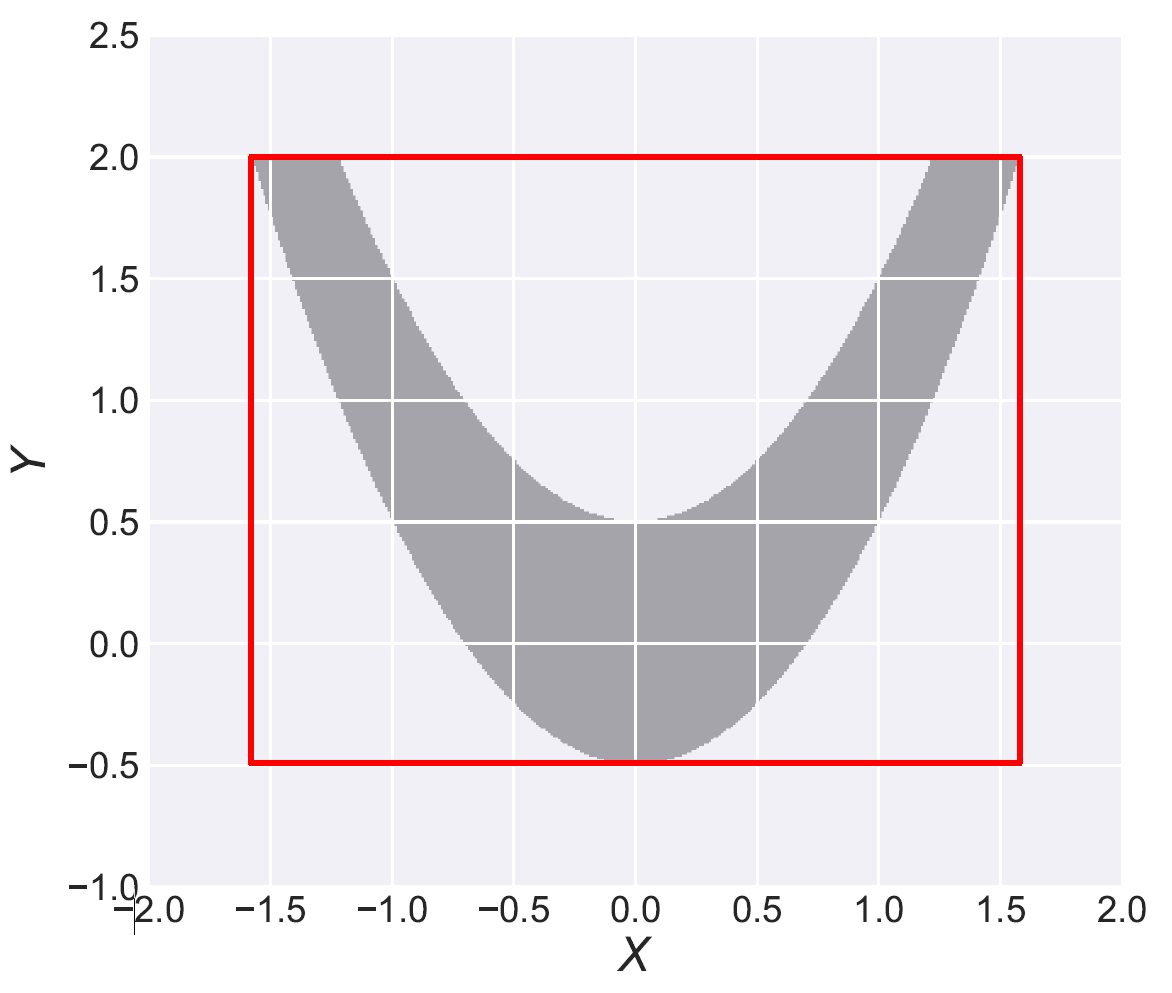The primary objective of this project is to establish innovative global optimization techniques that can effectively handle highly non-convex structures, disconnected feasible regions, and objective functions that are expensive to evaluate. To achieve this, our team constructed a novel spatial branching scheme based on convex relaxations. This scheme replaces the objective function with a convex underestimator, transforming it into a globally solvable convex program. Through iterative spatial branching, we utilize the solution of this convex problem to establish bounds and progressively reduce the optimality gap until epsilon-optimality is achieved. The success of our 
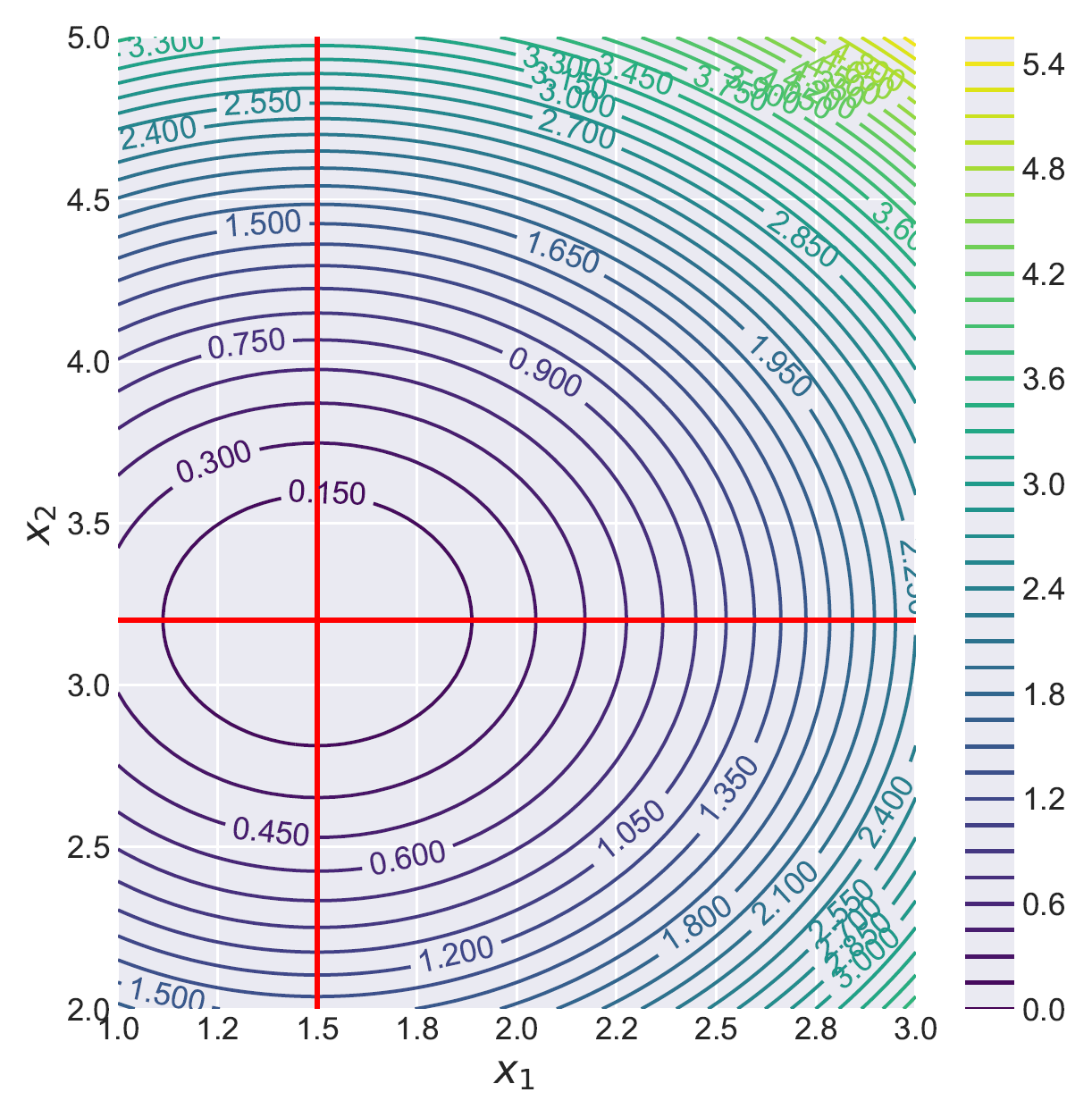implementation depends on striking a balance between convergence speed and computational cost. This presents a challenge due to the trade-off between tight and loose underestimators. Loose underestimators slow down convergence, while tight ones increase computational requirements. A pivotal advancement in this project is the introduction of a new class of parameterized convex underestimators that provide natural lower bounds and exact values at the feasible boundary. By extending Gershgorin’s theorem to interval matrices and leveraging interval arithmetic techniques, we ensure convexity and enable the efficient construction of tight convex underestimators. Our team has established theoretical guarantees that ensure the convergence of these underestimators to the original function, thereby guaranteeing the convergence of the spatial branching procedure to the global optimal solution. The proposed approach is highly generalizable, and in this project, we investigate two distinct applications of this work, which are highlighted below.
Characterizing the Mechanical Behavior of Materials
In this application, our team collaborates with material scientists and national laboratories to apply the established spatial branching technique for accurately calibrating mechanical constitutive models. Such models, which describe the fundamental mechanical response of materials, form the foundational blocks for solid mechanics simulations used in various applications. Recent technological advances have enabled highly sophisticated experimental designs, allowing for the full-field characterization of material responses in real time. Coupled with new developments in optimization, data processing, and high-performance algorithmic approaches, these advancements facilitate the construction of a mathematical framework that calibrates constitutive models in significantly less time and at a reduced cost. Central to this inverse 
characterization approach is a complex, non-convex optimization problem that must be solved to global optimality to achieve accurate parameter estimates. We implement the established spatial branching procedure to address this underlying challenge, characterizing the mechanical behavior of materials with an unprecedented level of accuracy. In doing so, we gain a deeper understanding of the complex mechanical behavior of both existing and new materials. Additionally, we quantify the margins in model parameters arising from both extrinsic experimental uncertainties and intrinsic material variations. This knowledge will pave the way for faster and more accurate predictions of material mechanics, advance the design of engineered materials, and accelerate the discovery of novel materials.
Constructing Robust Mass Screening Strategies
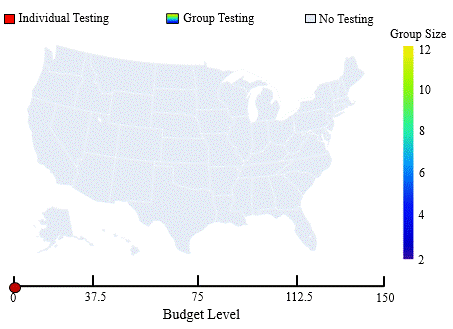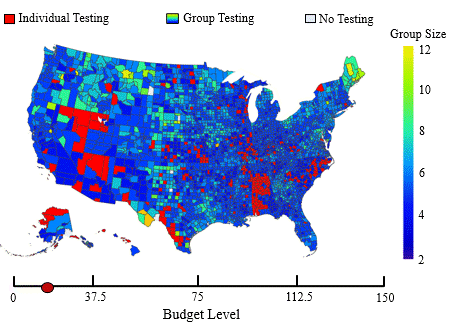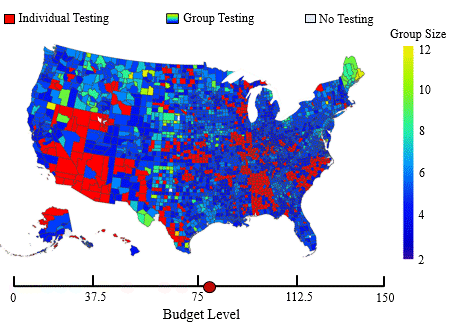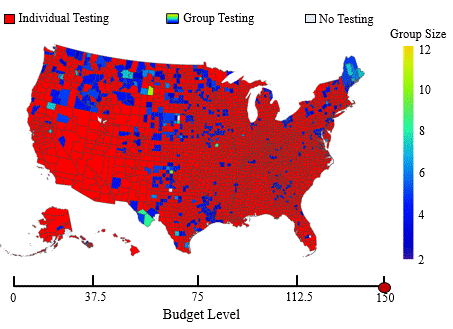
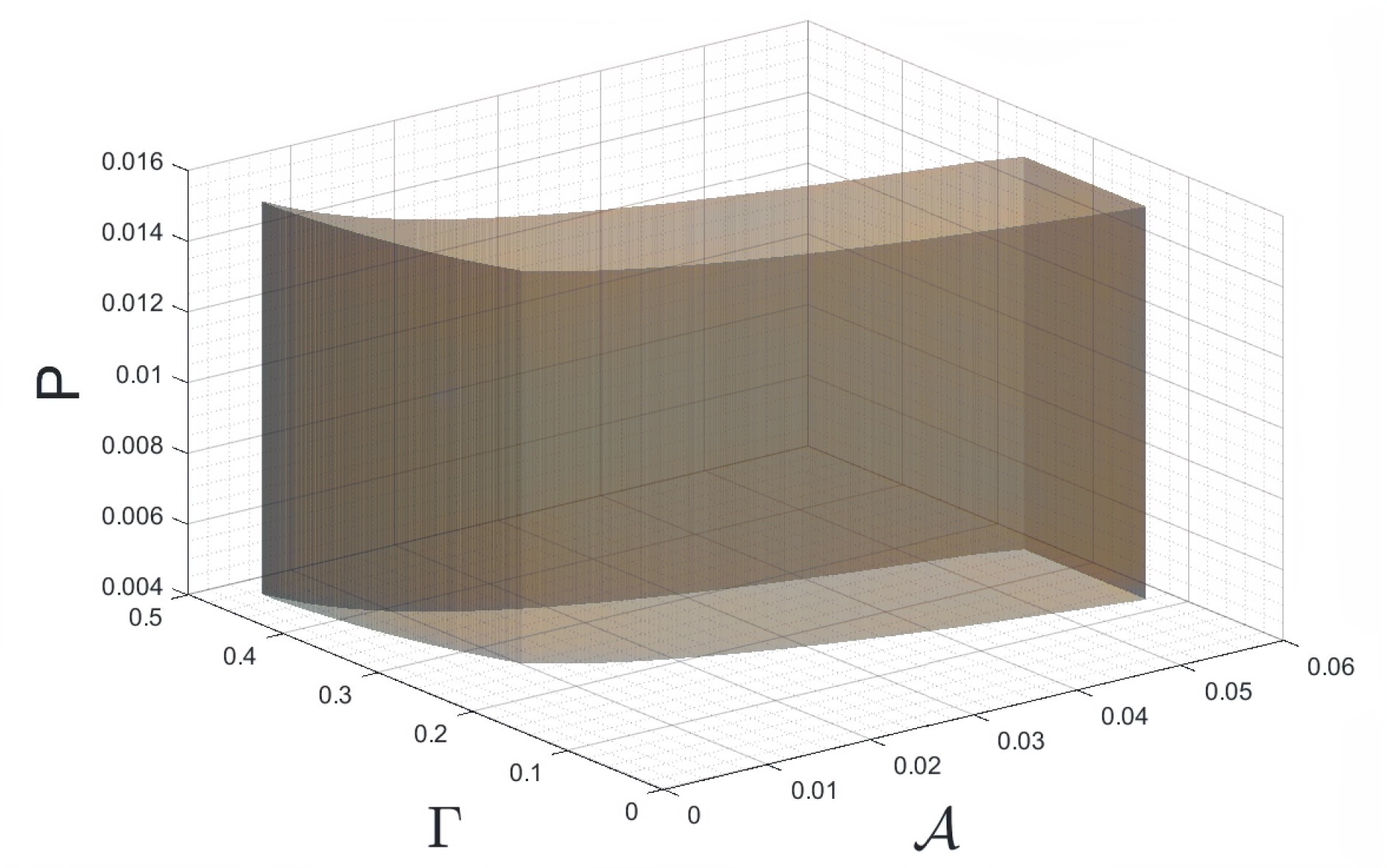
In this application, we adopt the established spatial branching technique to construct globally optimal, robust mass screening strategies that maintain effectiveness across a wide range of uncertain conditions. Mass screening of populations is an indispensable public health tool extensively utilized in various settings, such as screening for blood transfusions, gastric cancer, and sexually transmitted diseases (STDs). The primary objective is to efficiently screen a vast population to accurately classify them as positive or negative for the presence of an infectious agent. Due to the advent of the COVID-19 pandemic, the topic of mass screening has garnered considerable attention, being a pivotal aspect in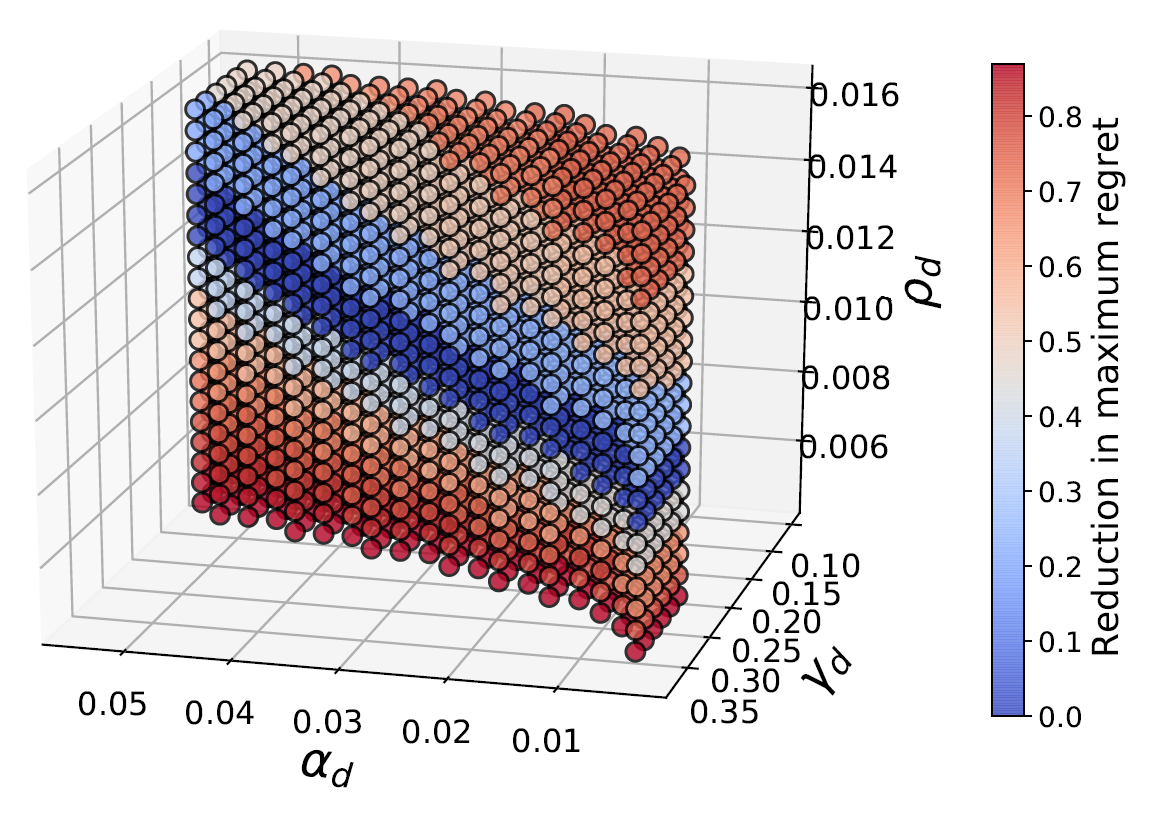 
effectively mitigating the spread of infectious diseases. However, high levels of uncertainty in numerous parameters make the establishment of effective mass screening strategies challenging. Constructing robust strategies guaranteed to perform well across various conditions is highly desirable as it ensures the proper performance of the deployed methods, regardless of the unobservable parameter values. To achieve this, we formulate the problem as a minimax regret-based optimization problem with a non-convex uncertainty set (see figure to the right), which presents a challenging nonlinear programming problem. Yet, due to the versatility of our spatial branching approach, we can adapt it to solve the underlying problem to global optimality. Our results lead to mass screening strategies that consistently outperform conventional, non-robust approaches over a broad range of conditions (see figure to the left), while also reporting extremely low “price of robustness” values.